数据结构与算法：拓扑排序

拓扑排序

一些概念

1. 有向无环图：有向说明图的路径是有方向的，无环说明图的路径不能成环。
2. 拓扑序列：设一个具有n个顶点的有向图，其中顶点序列V1—Vn满足一条路径，若Vi必须在Vj之前，则称这个顶点序列为拓扑序列。
3. 拓扑排序：按照顶点的依赖关系进行排序，使得没有前驱的顶点排在最前，没有后继的顶点排在后面，直到所有节点都被移除。

算法思想

它的思路总结起来只有两步：

1. 在有向图中选择一个没有前驱的顶点并输出。
2. 删除该顶点和以它为尾的弧。
3. 重复上述两步直到所有顶点都被输出，或者当前图中不存在无前驱的顶点为止。

算法实现

模拟实现

以下图中的图为例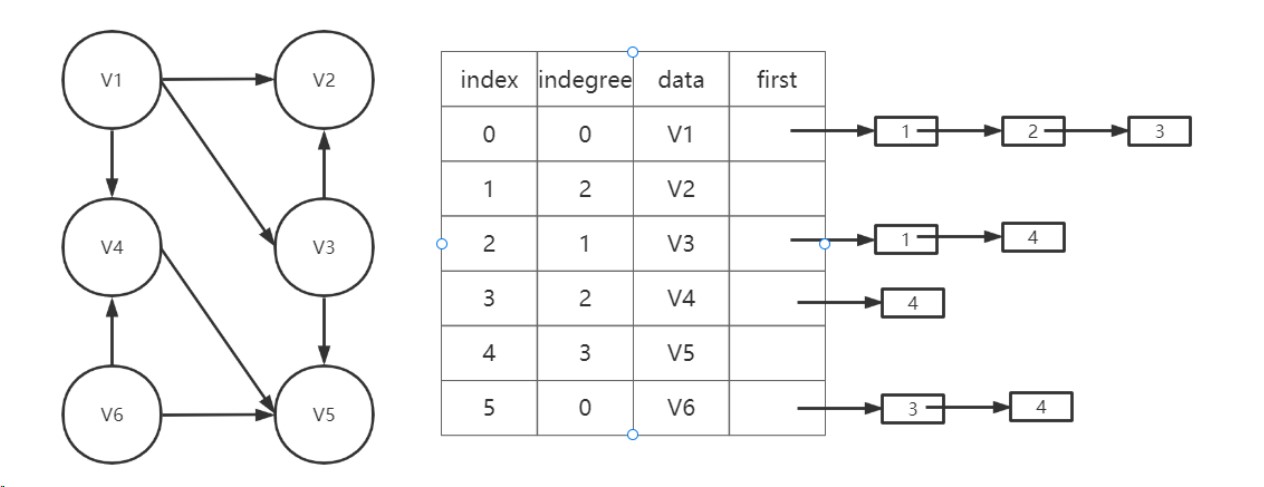

我们按照上述步骤进行模拟。

首先遍历寻找入度为0的顶点，即V1，输出V1，并删除以V1为尾的弧。
并再次遍历寻找入度为0的顶点，即V6，输出V6，并删除以V6为尾的弧。
遍历，找到V4的入度为0，输出V4，并删除以V4为尾的弧。
遍历，找到V5的入度为0，输出V5，并删除以V5为尾的弧。
遍历，找到V4的入度为0，输出V4，并删除以V4为尾的弧。
最后输出V2。
再次寻找发现所有顶点都被输出，完成排序。

代码实现

定义以下结构：
为了方便实现选用邻接表
Arr作为输出数组
Edge表示以Vi为弧尾的顶点组成的数组

#define MaxVertex 100
struct Graph
{
    int Data;
    int InDegree;
    int* Edge;
    int Size;
};

Graph G[MaxVertex];
int Arr[MaxVertex];

实现：

void TopologicalSort(Graph& G)
{
    int Count=0;
    while(Count<MaxVertex){
        for(int i=0;i<MaxVertex;i++){
            if(G[i].InDegree==0){
                Arr[Count++]=G[i].Data;
                for(int j=0;j<G[i].Size;j++){
                    G[G[i].Edge[j]].InDegree--;
                }
                break;
            }
        }
    }
}

使用栈实现：
与上述实现相似，先遍历寻找所有入度为0的顶点，输出栈顶元素，并移除以该顶点为尾的弧，然后再次遍历寻找所有入度为0的顶点，继续输出栈顶元素，直到所有元素都被输出，或者当前图中不存在无前驱的顶点为止。

vodi TopologicalSort(Graph& G)
{
    int Count=0;
    stack<int> s;
    while(Count<MaxVertex){
        for(int i=0;i<MaxVertex;i++){
            if(G[i].InDegree==0){
                s.push(G[i].Data);
            }
        }
        while(!s.empty()){
            Arr[Count++]=s.top();
            int v=s.top();
            s.pop();
            for(int i=0;i<G[v].Size;i++){
                G[G[v].Edge[i]].InDegree--;
                if(G[G[v].Edge[i]].InDegree==0){
                    s.push(G[v].Edge[i]);
                }
            }
        }
    }
}

• 本文作者： KongXinQing
• 本文链接： https://13114987559.github.io/2023/09/20/note/数据结构与算法-拓扑排序/
• 版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！