数据结构与算法：归并与统计排序

归并排序

算法思想：先将需要排序的元素分开，在合并的过程中将元素进行排序，最终得到一个有序数组。
分开方法：逻辑二分。

模拟：将数组拆分为单个元素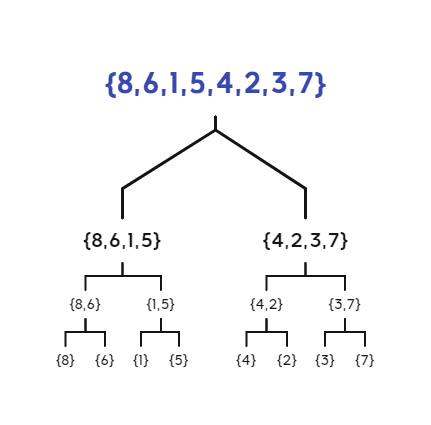

合并时按升序合并：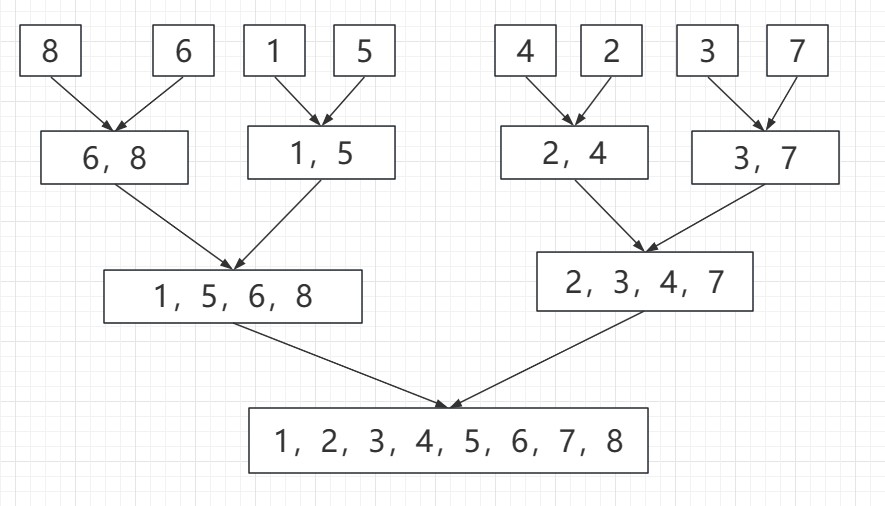

代码实现：

void Merge(int* arr,int left,int mid,int right)
{
    int k=0;
    int i=left;
    int j=mid+1;
    vector<int> temp(right-left+1);
    while(i<=mid && j<=right){
        if(arr[i]<arr[j]){
            temp[k++]=arr[i++];
        }else{
            temp[k++]=arr[j++];
        }
    }

    while(i<=mid){
        temp[k++]=arr[i++];
    }

    while(j<=right){
        temp[k++]=arr[j++];
    }

    for(int i=0;i<k;i++){
        arr[left+i]=temp[i];
    }

    
}

void MergeSort(int* arr,int left,int right)
{
    if(left>=right){
        return;
    }
    int mid=(right-left)/2 + left;
    MergeSort(arr,left,mid);
    MergeSort(arr,mid+1,right);

    Merge(arr,left,mid,right);
}

传入的参数为左闭右闭

统计排序

算法思想：先统计每个元素出现的次数，再根据次数进行排序。

计数排序

使用一个count数组作为计数数组，count[i]表示元素i出现的次数。
出现几次就输出几次下标。

缺点：当最大值过大时且元素总数不大时会极大的造成空间浪费；不能排小数。
优化：可以找到最大值和最小值进行优化，增加一个偏置值，但也只能部分优化，依然无法完全避免空间浪费。

代码很简单，就不写了(doge)

桶排序

算法思想：将元素划分到不同的桶中，每个桶中的元素进行排序，最后将桶中的元素合并。
例如可以每10为一组，将0-10为一个桶，10-20为一个桶，20-30为一个桶，以此类推再对桶内元素排序，整体就是有序的了。
缺点：有空间浪费，而且在某种情况下空间浪费会极大。

代码也很简单，就不写了(>_<)

基数排序

计数排序用于解决计数排序空间浪费的问题。

思路：按照位数进行计数排序，先按照个位进行排序，再按照十位进行排序，再按照百位进行排序，以此类推。位数不够则补零。

这个基本没什么用，代码就不写了（

• 本文作者： KongXinQing
• 本文链接： https://13114987559.github.io/2023/09/20/note/数据结构与算法-归并与统计排序/
• 版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！