数据结构与算法：图

字数统计: 2.5k字   |   阅读时长≈ 9分

图的概念

图（Graph）是由一组顶点(V)和一组能够将两个顶点相连的边(e)的非空有限集组成的。

例如：

定义一个图G=(V,E)，V={V1,V2,V3,V4},E={E1,E2,E3,E4,E5,E6}
E1=<V1,V2> E2=<V1,V3> E3=<V1,V4> E4=<V2,V3> E5=<V3,V2> E6=<V3,V3>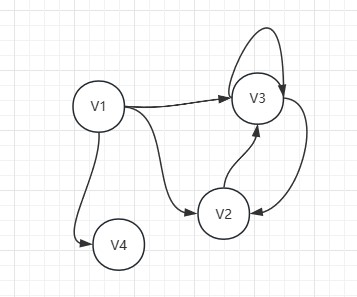

一些定义

基本概念

  1. 有向边：一条边所代表的顶点是有序的，则为有向边，也称弧，例如< V1,V2 >和< V2,V1 >是不同的两个边或弧。
  2. 无向边：一条边所带表的顶点是无序的，则为无向边，例如(V1,V2)和(V2,V1)是同一个边。
  3. 弧的头尾：一条边从V1指向V2，则V1为弧尾，V2为弧头。
  4. 度：一个顶点的度是指与它相连的边的数目，入度指入边数，出度指出边数。
  5. 路径：从顶点V1到V2的路径是指从V1到V2的边所表示的顶点序列。
  6. 权值：与图的边相关的数称为权值，带权值的图称为网。
  7. 连通：若两个顶点之间存在路径，则称这两个顶点是连通的。

图的分类

  1. 简单图：不存在顶点到自身的边且一条边不重复出现，这样的图称为简单图。
  2. 无向图：图中任意一条边代表的顶点是无序的，则为无向图。
  3. 有向图：图中任意一条边代表的顶点是有序的，则为有向图。
  4. 完全图：图中任意两个顶点之间都存在边，则为完全图。
  5. 连通图：图中任意两个顶点之间都存在路径，则为连通图，否则为非连通图。

图的存储

邻接矩阵

使用一个一维数组存储顶点信息，使用一个二维数组存储边信息。

结构如下：

顶点数组 V0 V1 V2 V3
V0 V1 V2 V3
V0
V1
V2
V3

无向图

对于无向图，若V1、V2之间存在边，则表中第一行第二列和第二行第一列的值为1，若不存在则为0.

特点：

  1. 表是对称矩阵。
  2. 某个顶点的度就是顶i行（或第i列）所有元素之和。

有向图

对于有向图，若V1、V2之间存在边，则表中第一行第二列的值为1，若不存在则为0。

特点：

  1. 表不对称，即第一行和第二行所代表的边不同。
  2. 要考虑出度和入度，顶点的出度是顶i行所有元素之和，顶点的入度是顶i列所有元素之和。

带权图

权值可以是任意值，所以对于带权图，若两点之间不存在边，则赋值为无穷大，否则赋值为权值。
假设权值是int类型，则使用INT_MAX表示边不存在。

邻接表

使用邻接矩阵的空间浪费较大，因此可以使用邻接表来存储图。

结构：使用一维数组或链表存储顶点信息，使用链表存储边信息。

无向图

假设有无向图G=(V,E)
V=(V0,V1,V2,V3)
E=(V0,V1),(V0,V2),(V0,V3),(V1,V2),(V2,V3)
其表示如下：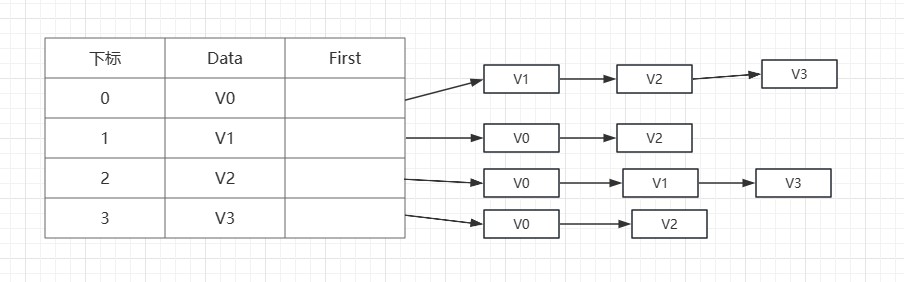

有向图

假设有有向图G=(V,E)
V=(V0,V1,V2,V3)
E={<V0,V1>,<V0,V3>,<V1,V0>,<V1,V2>,<V2,V0>,<V2,V3>}
以边表为弧头，就有以下结构：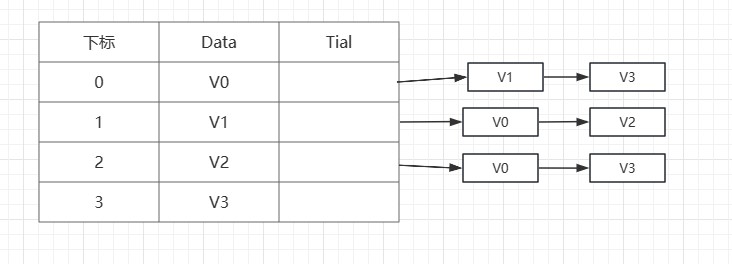

使用边表作为弧头容易统计出度，但不容易统计入度；使用边表作为弧尾，则容易统计入度，但不容易统计出度。

带权图

假设有有向图G=(V,E)
V=(V0,V1,V2,V3)
E={<V0,V1>=4,<V0,V3>=6,<V1,V0>=3,<V1,V2>=2,<V2,V0>=5,<V2,V3>=8

同样以边表为弧头，则有：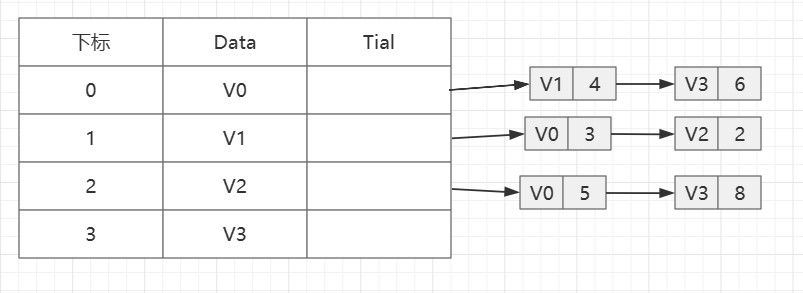
}

十字链

十字链表是把邻接表和逆邻接表结合在一起的一种结构，有如下例子：
！

我们定义如下结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct Vertex
{
    int V;
    int FirstIn;
    int FirstOut;
};

struct EdgeList
{
    int TialVertex;
    int HeadVertex;
    int HeadLink;
    int TailLink; 
}

在顶点结构中FirstIn表示顶点的第一个入边，FirstOut表示顶点的第一个出边,V代表顶点。
在边表结构中TailVertex表示狐尾顶点，HeadVertex表示弧头顶点，HeadLink表示弧头相同的下一条弧，TailLink表示弧尾相同的下一条弧。

按照上述进行连接后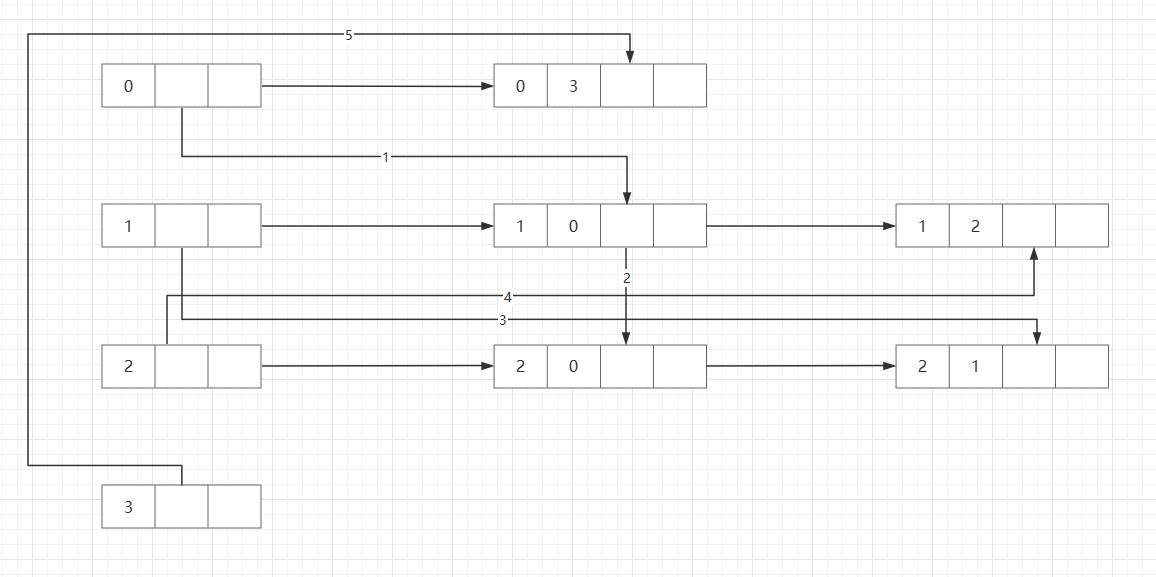

除标线数字外来接边表，并将第一个数（TailVertex）初始化为顶点下标。
对于第一行以0为弧尾的顶点为V3，所以第二个数填为3，第二第三行同理，因为没有以V3为弧尾的顶点，所以第四行填0。

接下来连线。
以V0为弧头的顶点有V1、V2，所以V0所在行出一条线连接V1行V2行所在边表中的顶点V0（数字0），连接好后就得到编号1、2的两条边。
以V1为弧头的顶点只有V2，所以V1所在行顶点出一条线连接V2行所在边表中的顶点V1（数字1），连接好后就得到编号3边。
以V2为弧头的顶点只有V1，所以V2所在行顶点出一条线连接V1行所在边表中的顶点V2（数字2），连接好后就得到编号4边。
以V3为弧头的顶点只有V0，所以V3所在行顶点出一条线连接V0行所在边表中的顶点V3（数字3），连接好后就得到编号5边。
通过以上步骤就得到一个十字链表。

邻接多重表

邻接多重表与十字链表类似，我们定义以下结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
struct Virtex
{
    int V;
    int Edge;
};

struct EdgeList
{
    int iVertex;
    int iLink;
    int jVertex;
    int jLink;
};

iLink和jLink表示依附于iVertex和jVertex的顶点下标，作为中转点存在。

以下图为列：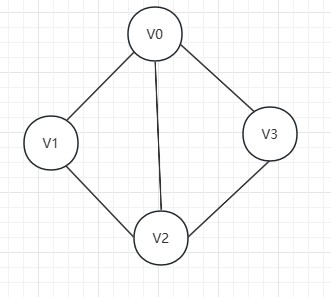

连接后过程与十字链表类似，连接后得到如下图：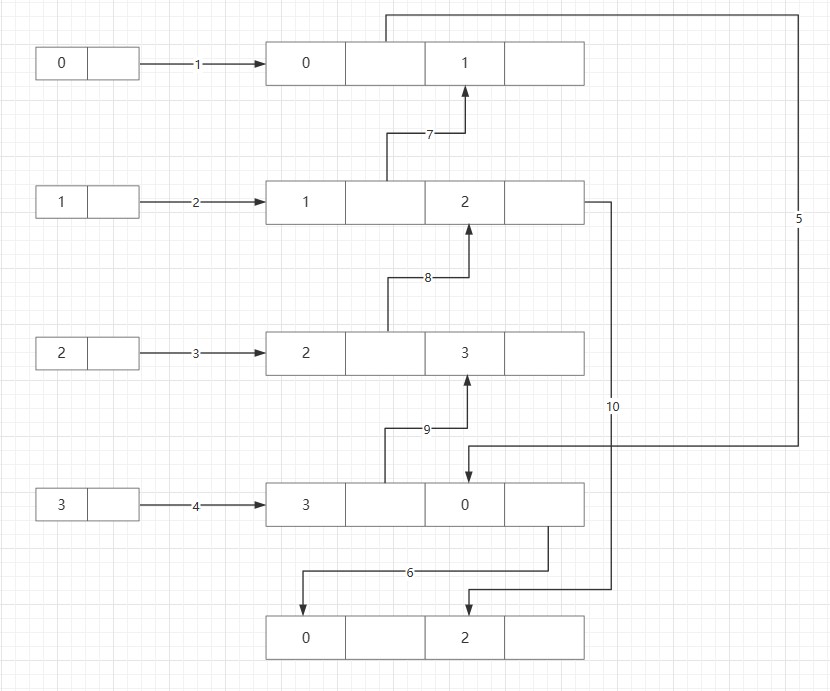

具体连接过程如下：
首先连接1、2、3、4四条边。
对于V0来说，有3条边(V0,V1)、(V0,V2)、(V0,V3),第一行已经连接了(V0,V1)，连接(V0,V2)(V0,V3)时，可以先寻找V3行中依附于V0的边将其连接，对于V2可以使用最后一行来寻找，它同样可以在V3行中找到。
对于V1，有两条边，(V1,V2)、(V1,V0)，在V0行寻找V1顶点，从最后一行寻找V2顶点。
对于V2，有三条边，(V2,V1)、(V2,V0)、(V2,V3)，(V2,V3)已经连接，在V1行寻找V2顶点，再从V1行向最后一行寻早V2顶点。
对于顶点V3，有两条边，(V3,V0)、(V3,V1)，已经连接了(V3,V0),在V2行寻找V3顶点并连接。
最后得到1-10条边。

边集数组

由两个一维数组组成，其中一个储存顶点信息，另一个数组存储边信息，边信息包括边的起点和终点以及权值（如果有的话）。

结构定义如下

1
2
3
4
5
6
7
8
9
int Vertex[MaxVertexNum];
struct Edge
{
    int start;
    int end;
    int weight;
};

Edge EdgeArray[MaxVertexNum];

图的遍历

深度优先遍历

深度优先遍历，简称DFS，是从初始结点出发，沿着一条路一直走到底，再回溯，再走下一条路，直到走完所有路。
简单来说就是从开始一条路走到底，没有路时回溯一步继续走下一条路。
从定义可以看出深度优先遍历与树的前序遍历相似，所以可以使用栈实现DFS。

思路：

  1. 从顶点开始，走过的路写上记号。
  2. 走向离自己最近的未走过的节点。
  3. 当这条路没有路时（即没有可以访问的节点），回溯一步，访问还未走过的节点。
  4. 重复2、3，直到所有节点都访问过。

代码实现(使用邻接表)：

1
2
3
4
5
6
7
8
9
10
11
12
13
//定义结构
struct Vertex
{
    int Vertex;
};

struct Graph
{
    int Data;
    Vertex* V;
};

Graph G[MaxVertexNum];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
//递归实现
bool Vistied[MaxVertexNum]={0};
//顶点是否访问，1为访问，0为未访问

void DFS(Graph& G, int v)
{
    //V为当前顶点下标，G为图
    if(Vistied[v]==true){
        return;
    }

    cout << G[v].Data << " ";
    Vistied[v]=true;

    for(int i=0;i<MaxVertexNum;i++){
        if(G[v].V[i].Vertex!=-1 && Visited[G[v].V[i].Vertex]==false){ 
            DFS(G,G[v].V[i].Vertex);
        } 
    }
}

//栈实现
void DFS(Graph& G)
{
    stack<int> s;
    int v=0;
    s.push(v)；
    while(!s.empty()){
        int v=s.top();
        if(Visited[v]==false){
           Visited[v]=true;
           cout << G[v].Data << " ";
        }

        for(int i=0;i<G[v].size();i++){
            if(Visited[G[v].V[i].Vertex]==false){
                s.push(G[v].V[i].Vertex);
                break;
            }
            if(i==G[v].size()-1){
                s.pop();
                //此时G[v].V[i].Vertex已经全部访问过，进行回溯
            }
            
        }          
    }
}

广度优先遍历

广度优先遍历，简称BFS，从初顶点出发，首先访问该顶点所有相连的顶点，然后依次访问这些顶点相连的顶点。
遍历顺序与树的层序遍历类似，可以使用队列实现。

思路：

  1. 将初始顶点入队。
  2. 访问队首顶点，并将其所有与它相连的顶点入队，并弹出该顶点。
  3. 重复步骤2，知道队列为空。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void BFS(Graph& G)
{
    queue<int> q;
    q.push(0);
    while(!q.empty()){
        int v=q.front();
        q.pop();

        if(Visited[v]==false){
            cout << G[v].Data << " ";
            Visited[v]=true;
        }
          
        for(int i=0;i<G[v].size();i++){
            if(Visited[G[v].V[i].Vertex]==false){
                q.push(G[v].V[i].Vertex);
            }
        }
    }
}

总结

第一部为图的一些基本概念和定义。
第二部分为图的存储结构。
第三部分为图的遍历。

关于图的另一些算法，如最小生成树、最短路径、关键路径、拓扑排序等，会在后续文章中介绍。

扫一扫，分享到微信

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia-plus根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true


个人简介:
大学生一枚，想要从事游戏开发,
希望能做出自己的游戏

主要涉及技术：
UE4、Unity2D、C++