数据结构与算法：二叉树

字数统计: 2.5k字   |   阅读时长≈ 10分

树

树的定义

树是n(n>=0)个结点的有限集合，当n=0时，称为空树。在任意一棵非空树中：

  1. 有且仅有一个特定的称为根的结点。
  2. 当n>1时，其余结点可分为m(m>0)个互不相交的有限集，每个集合本身又是一棵树，称为原树的子树。

树的相关概念

  1. 节点的度：节点拥有的子树个数称为节点的度。
  2. 节点的深度：从根开始往下，逐层累加，根的深度为0。
  3. 森林：由m(m>=0)棵不相交的树的集合称为森林。

树的存储结构

双亲表示法

用一组连续空间存储树中的节点，同时在每个节点中，附设一个指示器指示其双亲结点在数组中的位置。

节点定义如下

1
2
3
4
5
struct Node
{
    int Data;
    int Parent;
};

孩子表示法

孩子表示法是将每个节点的孩子结点排列起来，形成一个线性结构，然后用链表建立节点与孩子结点之间的关联关系。

孩子链表的定义如下

1
2
3
4
5
struct Node
{
    int Data;
    struct Node *FirstChild;
};

孩子兄弟表示法

孩子兄弟表示法是将每个节点的孩子结点排列起来，形成一个线性结构，然后用指针来建立节点与孩子结点之间的关联关系。

节点定义如下

1
2
3
4
5
6
struct Node
{
    int Data;
    struct Node *FirstChild;
    struct Node *NextSibling;
};

二叉树

定义

  1. 每个节点最多有两个孩子结点，分别称为左孩子和右孩子。
  2. 每个节点最多有一个双亲结点。
  3. 除根结点外，其余每个结点又包含一个零或两个以上的子树。

特殊的二叉树

  1. 斜树：所有节点均为左子树或右子树的二叉树。
  2. 满二叉树：除叶子节点外所有节点均有左右子树且所有叶子节点均在同一层上。
  3. 完全二叉树：除最后一层外，每一层节点数均达到最大值，且最后一层节点均连续集中在最左边。

二叉树的性质

  1. 在二叉树的第i层上至多有2^(i-1)个节点（i>=1）。
  2. 深度为k的二叉树至多有(2^k)-1个节点（k>=1）。
  3. 对于任意一棵二叉树T，如果叶子节点数为n0，度为2的节点数为n2，则n0=n2+1。
  4. 具有n个节点的完全二叉树的深度为[log2n]+1。

二叉树存储结构

顺序存储结构

用一组连续空间存储二叉树中的节点，用二叉树中结点在数组中的下标表示结点在二叉树中的位置。

节点定义如下，Data表示数据域，LeftChild表示左孩子下标，RightChild表示右孩子下标

1
2
3
4
5
6
struct Node
{
    int Data;
    int LeftChild;
    int RightChild;
};

链式存储结构

链式存储结构采用二叉链表存储结构，每个节点包括数据域和左右孩子指针。

节点定义如下

1
2
3
4
5
6
struct Node
{
    int Data;
    struct Node *LeftChild;
    struct Node *RightChild;
};

二叉树的遍历

先序遍历

递归遍历

1
2
3
4
5
6
7
8
9
void PreOrder(struct Node *Tree)
{
    if(!Tree)
    {
        cout << Tree->Data << endl;
        PreOrder(Tree->LeftChild);
        PreOrder(Tree->RightChild);
    }
}

迭代遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void PreOrder(struct Node *Tree)
{
    if(!Root){
        return;
    }
    stack<Node *> s;
    struct Node *p;
    s.push(Root);
    while(!s.empty()){
        p=s.top();
        cout << p->Data << " ";
        s.pop();
        if(p->Right){
            s.push(p->Right);
        }
        if(p->Left){
            s.push(p->Left);
        }
    }
}

中序遍历

递归遍历

1
2
3
4
5
6
7
8
9
void InOrder(struct Node *Tree)
{
    if(!Tree)
    {
        InOrder(Tree->LeftChild);
        cout << Tree->Data << endl;
        InOrder(Tree->RightChild);
    }
}

迭代遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void InOrder(struct Node *Tree)
{
    if(!Root){
        return;
    }

    stack<Node *> s;
    struct Node *p;
    while(!s.empty() || Root!=NULL){
        if(Root){
            s.push(Root);
            Root=Root->Left;
        }
        else{
            p=s.top();
            cout << p->Data << " ";
            Root=p->Right;
            s.pop();
        }
    }
}

后续遍历

递归遍历

1
2
3
4
5
6
7
8
9
void PostOrder(struct Node *Tree)
{
    if(!Tree)
    {
        PostOrder(Tree->LeftChild);
        PostOrder(Tree->RightChild);
        cout << Tree->Data << endl;
    }
}

迭代遍历（单栈）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void PostOrder(struct Node *Tree)
{
    if(!Root){
        return;
    }

    stack<Node *> s;
    struct Node *p=Root;
    struct Node* Temp;
    while(!s.empty() || p!=NULL){
        if(p){
            s.push(p);
            p=p->Left;
        }
        else{
            p=s.top();
            if(p->Right && Temp!=p->Right){
                p=p->Right;
            }
            else{
                cout << p->Data << " ";
                Temp=p;
                s.pop();
                p=NULL;
            }
        }
    }
}

迭代遍历（双栈）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void PostOrder(struct Node *Tree)
{
    if(!Root){
        return;
    }

    stack<Node *> s1,s2;
    struct Node *p;
    s1.push(Root);
    while(!s1.empty()){
        p=s1.top();
        s1.pop();
        s2.push(p);
        if(p->Left){
            s1.push(p->Left);
        }
        if (p->Right){
            s1.push(p->Right);
        }
    }
    while(!s2.empty()){
        cout << s2.top()->Data << " ";
        s2.pop();
    }
}

层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void LevelOrder(struct Node *Tree)
{
    queue<struct Node *> q;
    q.push(Tree);
    while(!q.empty())
    {
        struct Node *p = q.front();
        q.pop();
        cout << p->Data << endl;
        if(p->LeftChild){
            q.push(p->LeftChild);
        }
        if(p->RightChild){
            q.push(p->RightChild);             
        }
    }
}

线索二叉树

线索二叉树的定义

线索二叉树中有的节点指向左右孩子，有的节点指向前驱和后继，这种二叉树称为线索二叉树。

线索二叉树的实现

因为叶子节点没有左右孩子，所以对叶子节点进行特殊处理，将左指针指向后继，右指针指向前驱。
并且由于有的节点有左右孩子，所以在线索化是还要增加一个标志以表示当前节点指向左右孩子还是前驱后继。

代码实现

1
2
3
4
5
6
struct Node
{
    int Data;
    struct Node *LeftChild,*RightChild;
    int LTag,RTag;
};

以上是对节点的定义，LTag和RTag分别表示当前节点是左孩子还是右孩子且默认为0，如果Tag=0表示指向的是左孩子，如果Tag=1表示指向的是右孩子。

如何线索化

我们对二叉树进行某种遍历使其便为线索二叉树的过程称为线索化。

以中序遍历为例，线索化的过程如下：

  1. 如果当前节点没有左孩子，则左指针指向中序遍历的前驱，并且左指针的LTag置为1，表示指向前驱。
  2. 如果当前节点有左孩子，则左指针指向左孩子，并且左指针的LTag置为0，表示指向左孩子。
  3. 如果当前节点没有右孩子，则右指针指向中序遍历的后继，并且右指针的RTag置为1，表示指向后继。
  4. 如果当前节点有右孩子，则右指针指向右孩子，并且右指针的RTag置为0，表示指向右孩子。
  5. 如果没有前驱，则指向为NULL，如果没有后继，则指向为NULL。

代码实现（采用递归中序遍历）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Node *Pre;
void InThreading(Node *p)
{
    if(!p){
        return;
    }

    InThreading(p->LeftChild);

    if(!p->LeftChild){
        p->LeftChild = Pre;
        p->LTag = 1;
    }

    if(!p->RightChild){
        p->RightChild = Pre;
        p->RTag = 1;
    }

    Pre = p;

    InThreading(p->RightChild);
}

如何通过线索二叉树进行遍历

通过线索二叉树进行遍历的过程和二叉链表类似，但是由于线索二叉树中有的节点有左右孩子，有的节点有前驱和后继，所以遍历的过程需要对有左右孩子的节点和没有左右孩子的节点进行特殊处理。

代码实现（中序遍历）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void InOrder(Node *Root)
{
    Node *p=Root;
    while(p){
        while(p->LTag==0){
            p = p->LeftChild;
        }

        cout << p->Data << " ";

        while(p->RTag==1 && p->RightChild!=NULL){
            p = p->RightChild;
            cout << p->Data << " ";
        }
        p = p->RightChild;
    }
}

赫夫曼树

什么是赫夫曼树

赫夫曼树是带权路径长度最短的二叉树，也叫最优二叉树。

路径和路径长度：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

结点的权：给树中结点赋予一个数值，称为这个结点的权。权是表示结点重要程度的量。

结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积。

树的带权路径长度：所有叶子结点的带权路径长度之和。

构建赫夫曼树

  1. 从带权值的叶子节点小到大进行排序。
  2. 选择权值最小的两个节点，将这两个节点合并，较小的节点在左边，生成新的节点，并将新节点的权值设为这两个节点的权值之和。
  3. 重复步骤2，直到只剩下一个节点。

赫夫曼编码

赫夫曼编码是一种前缀编码（不能是另一字符串的前缀），赫夫曼编码的实现过程如下：

  1. 统计字符出现的次数，得到每个字符的权值。
  2. 按照权值从小到大的顺序，将所有的字符和权值形成一个数组。
  3. 初始化一个二叉树，将权值数组中的元素按照从左到右的顺序依次放入到二叉树中

假如有一段文本”ABDCADFEED“，使用二进制传输：

字母 A B C D E F
二进制 000 001 010 011 100 101

得到的二进制串为：000001011001000010101100100010

如果采用赫夫曼编码：
统计字母出现的频率，得到如下表格

字母 A B C D E F
频率 2 1 1 3 2 1
赫夫曼编码 011 100 101 11 00 010

频率表示
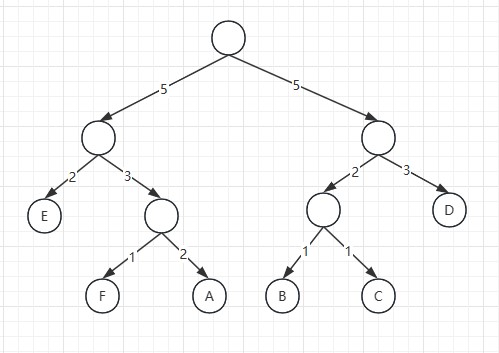
转为编码后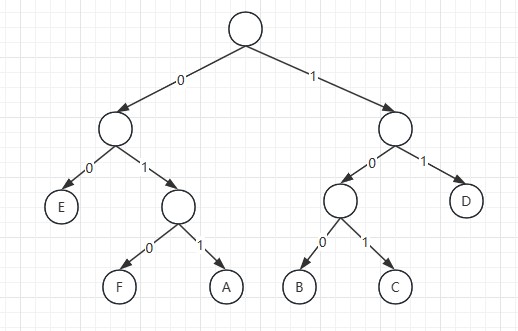
编码表示

总结

主要关于树、二叉树、线索二叉树、赫夫曼树的概念和实现，后续更新B树和红黑树。

扫一扫，分享到微信

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia-plus根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true


个人简介:
大学生一枚，想要从事游戏开发,
希望能做出自己的游戏

主要涉及技术：
UE4、Unity2D、C++